1. Mapping(매핑) : Changing Descriptions from Frame to Frame (한 계에서 다른 계로 표시를 변경)
- 로봇공학에서는 하나의 양을 여러 개의 다른 기준 좌표계에 대해서 표현할 필요가 있다.
(1) Mapping involving translated frames 전위(병진)된 계를 포함하는 매핑
- 좌표계가 회전없이 위치만 이동하는 것을 translation 병진, 전위한다 라고 한다.
아래 그림을 살펴보자.
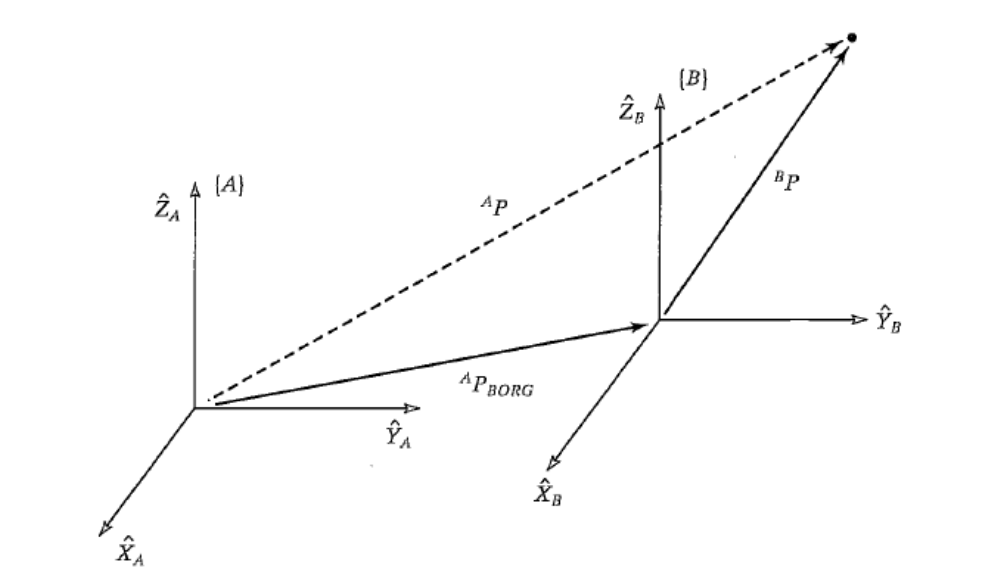
- Bp가 표현하는 점을 생각해보자. 이 점은 P이고 {B}를 기준으로 표현된다.
- 이 점 P를 {A} 기준으로 표현하려고 한다.
- {B}는 {A}와 같은 orientation(방위)을 가진다고 하자. 즉, {A}와 {B} 사이에는 회전이 없다.

- 위 식(*)은 프레임 {B}에서 표현된 벡터를 프레임 {A}에서 표현된 벡터로 변환하는 Mapping이다.
- 점 P는 변화하지 않는다.
- 점 P가 표현되는 기준 좌표계가 {B} 기준에서 {A} 기준으로 변경된다.
(2) Mapping involving rotated frames 회전된 계를 포함하는 매핑
- Rotation matrix (회전 행렬) 은 {B}의 방위를 {A} 기준으로 표현한다.
- 회전 행렬은 다음 특징을 갖는다.

- {B}는 {A}와 같은 원점을 가진다고 하자. 즉 {A}와 {B} 사이에는 병진이 없다. 점 P의 표현을 {B} 기준으로 알고 있을 때 이 점을 {A} 기준으로 표현하려면?

* 문제 1 : 아래 그림에서 {B}는 {A}를 {A}의 Z방향으로 30도 회전시킨 결과이다. Bp가 [ 0.0, 2.0, 0.0]으로 주어질 때 Ap를 계산하시오.
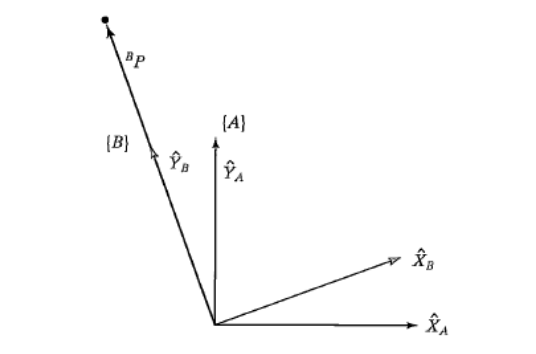

* 문제 2 : 문제 1에서 30도를 Θ도로 Bp를 [Px Py Pz]로 바꾸어서 풀이해라.
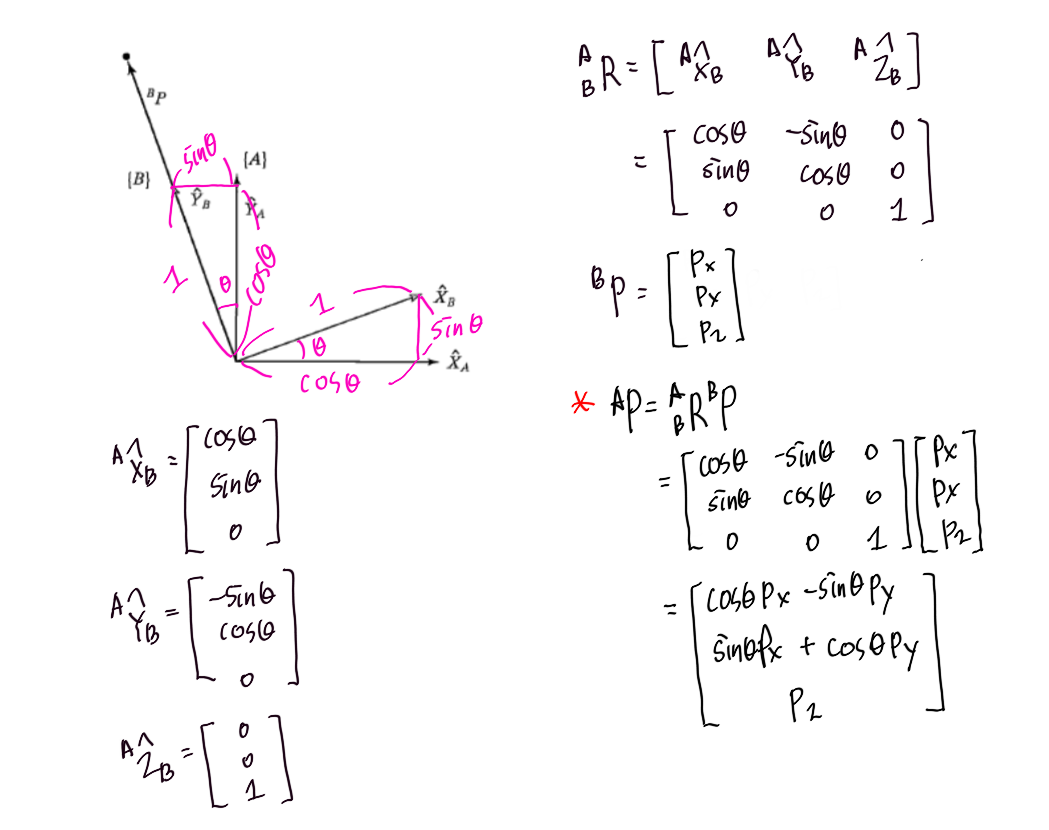
(3) Mapping involving general frames 일반적인 계를 포함하는 매핑 (회전과 병진 둘 다)
- 문제를 풀어보면서 알아보자.
* 문제 : {A}와 {B}의 원점과 방위가 서로 다르다. 점 P의 표현을 {B} 기준으로 알고 있을 때 이 점을 {A} 기준으로 표현하려면?

문제 해석 :
- 계 {B}의 원점은 일반적으로 계 {A}의 원점과 일치하지 않으며 일반적으로 벡터 오프셋(vector offset, {B} 원점이 {A} 원점에서 이동한 거리}을 갖고 있다.
- {B}의 원점을 {A}에 대해 표현한 벡터를 ApBORG로 표현한다.
- {B}가 {A}를 기준으로 회전한 양을 회전 행렬로 표현한다.
- 이 문제의 답은 2단계로 구한다.
1단계 : 원점은 {B}와 같고 방위는 {A}와 같은 프레임 {B'}을 생각하자. Bp를 {B'}에 대해 표현한다.
2단계 : {B'}과 {B'}은 원점은 같고 방위만 다르다. 점 P의 표현을 {B'}에서 {B}로 변경한다.
위의 2단계의 결과는 아래와 같다.

2단계 결과 식을 편리한 계산을 위해서 하나의 행렬을 이용한 변환식으로 표현 가능하다.

- 회전 행렬을 이용해서 회전을 표현하는 것처럼 변환을 이용해서 회전과 병진이 포함된 일반적인 프레임(계)을 표현한다.
* 문제 1 :



* 문제 2 : 문제 1에서 회전각도가 60도인 경우 Ap를 구해라. (회전각도를 제외한 모든 조건은 동일)

'기타 > 이것저것' 카테고리의 다른 글
| [GPU] NVIDIA 드라이버 & CUDA Toolkit 설치하기 / 2023.06.15 (0) | 2023.06.15 |
|---|---|
| 자바 환경변수 설정 (Windows) / 2023.06.02 (0) | 2023.06.02 |
| [로봇공학] 공간 표시(Position, Orientation, Frame) / 2021.10.17 (1) | 2021.10.17 |
| [로봇공학] 머니퓰레이터 좌표계 설정하기, 링크 파라미터 / 2021.10.11 (0) | 2021.10.11 |
| [GitHub] 웹호스팅, 웹페이지 배포 / 2021.10.08 (0) | 2021.10.08 |



